The Ins and Outs of Math Terms: A Glossary

Counting and quantities are building blocks to higher math skills, such as order of operations and geometry. Terms found in a counting and cardinality list include:

• array - set of numbers or objects in rows and columns
• cardinal numbers (cardinality) - number words that mark quantity (e.g. one, two, three)
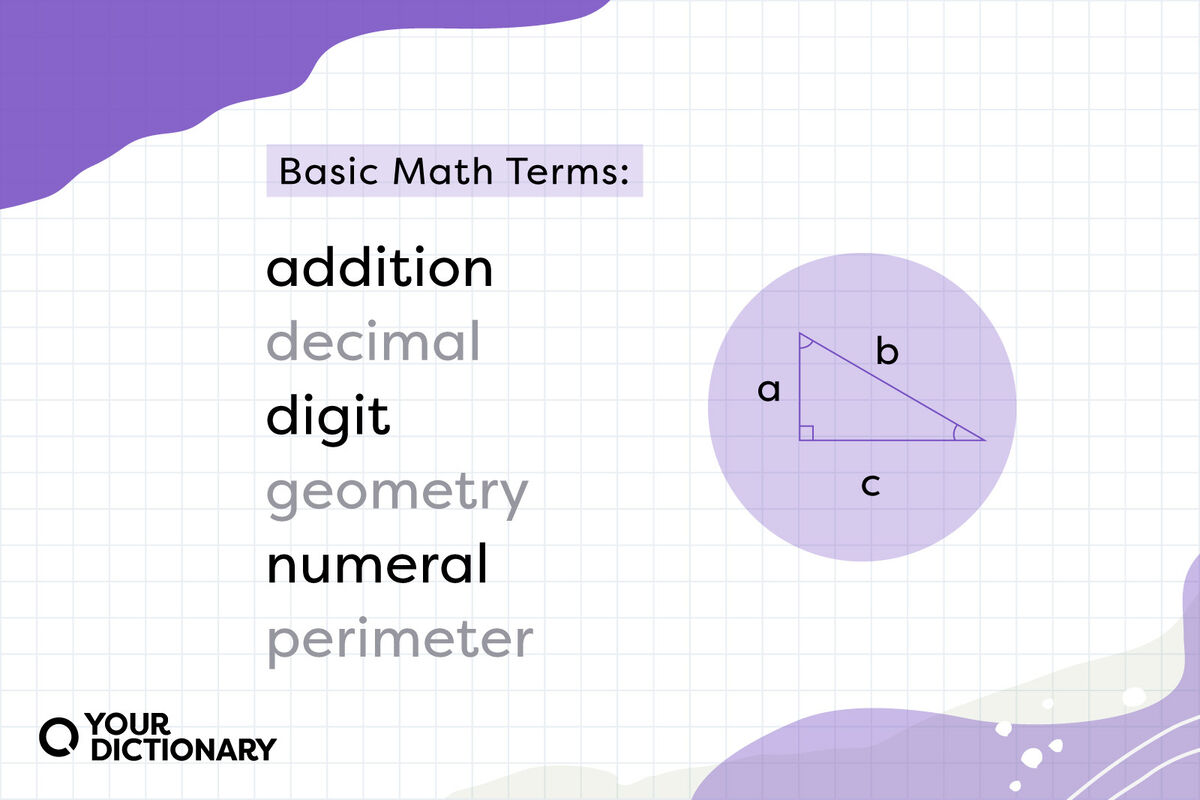
• digits - numerals found in all numbers; includes one-digit numbers (e.g. 0, 7, 4) and multi-digit numbers (e.g. 12, 284, 5746)
• equal - having the same value
• greater than - having a higher value
• less than - having a lower value
• numeral - written symbol that indicates a value (e.g. 1, 2, 3)
• one-to-one correspondence - understanding that numbers correspond to quantities (e.g. five apples, sixteen cars)
• ordinal numbers (ordinality) - number words that mark an item’s position in a sequence (e.g. first, second, third)
• sequence - collection of numbers or objects in a particular order

Addition, subtraction, multiplication, and division are known as the order of operations. Students need to know the basic terms for these skills, including:

• addend - the two numbers added together in an addition problem
• addition - combining two numbers to make a new total (sum)
• algebra - branch of mathematics in which students solve for the value of variables (symbols or letters)
• arithmetic - the study of numerical quantity using counting and operations (addition, subtraction, multiplication, division)
• associative property - mathematical property by which three or more numbers can be grouped in any way and still have the same sum (addition) or product (multiplication)
• average (mean) - the sum of numbers divided by the count of numbers
• commutative property - mathematical property that states that numbers can be added or multiplied in any order and still have the same answer
• compose - putting a number back together from sets of ones, tens, hundreds, etc.
• composite number - any number that can be divided by more numbers than 1 and itself (opposite of a prime number)
• difference - the result of a subtraction problem
• distributive property - mathematical property by which the sum of two numbers multiplied by a third number is equal to the products of the first two numbers individually multiplied by the third number
• dividend - number being divided into parts
• division - process of dividing one number into a set number of parts
• divisor - number that divides the dividend into parts
• equation - number statement that shows two equal expressions on either side of an equal sign
• even number - any number that is divisible by 2
• factor - number that divides into another exactly (e.g. 3 is a factor of 12)
• formula - equation that describes the consistent relationship between variables (e.g. the formula for volume: V = lwh)
• identity property - mathematical property by which the sum of any number and 0 is itself (in addition), and the product of any number and 1 is itself (multiplication)
• integer - whole number (including zero)
• minuend - the top number in a subtraction equation; the number that is subtracted from
• multiplicand - each number in a multiplication problem
• multiplication - repeated addition of one number a set amount of times
• odd number - any number that can’t be divided by 2
• operation - addition, subtraction, multiplication, or division
• order of operations - the order in which you solve an algebraic equation (Parentheses, Exponents, Multiplication, Division, Addition, Subtractions — also known as PEMDAS)
• parentheses (also brackets or braces) - symbols that indicate multiplication in an equation, or group numbers to be calculated first in the order of operations
• product - the result of a multiplication problem
• prime number - number that is only divisible by itself and 1
• quotient - result of a division problem
• remainder - the amount left over when a divisor does not divide evenly into a dividend
• subtraction - one number minus or taking away another number.
• subtrahend - the number subtracted from the first number in a subtraction problem
• sum - the result of an addition problem
• variable - letter that represents the value that one must solve an equation to find
• whole number - a number without fractions; a number that has all the parts of a whole

Basic number and operations concepts include base ten, fractions, place value, and decimals. Math terms in this glossary category include:

• algorithm - a procedure that carries an operation out in steps
• base ten - number system (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) in place value positions
• decimal - real number from the base 10 number system that represents a fraction using place value (e.g. 2.73, 0.453)
• denominator - the bottom part of a fraction; how many parts are in a whole
• equivalent - equal in value or amount
• expanded form - way of writing out a multi-digit number by its place value (e.g. the expanded form of 736 is 700 + 30 +6)
• exponent - superscript number that indicates repeated multiplication of a number
• fraction - a number that is not whole; one part (numerator) is present over the whole (denominator)
• irrational number - number than cannot be expressed as a decimal because its digits are infinite (e.g. π)
• mixed number - whole numbers combined with fractions (e.g. 3 ¼)
• non-zero - number that is not zero
• number line - line with positive and negative numbers assigned to various points
• numerator - top part of a fraction; the part present of a whole
• place value - numerical value of a digit based on its position in a number (e.g. tens place, hundredths place)
• rational number - number that can be expressed as a fraction or decimal

Measurement and data includes measuring the attributes of a shape to find its area, volume, mass, or perimeter. It also includes measuring time, creating bar graphs, and calculating amounts of money. Common measurement and data terms include:

• analog clock - traditional clock face with hour, minute, and second hands
• area - two-dimensional space taken up by a shape (measured in square units)
• bar graph - visual representation of data using bars of different heights or widths
• cubic unit - unit cube; unit for measuring volume in three-dimensional spaces
• data point - unit of information that can be graphed
• data set - collection of data points that can be graphed
• digital clock - clock that displays the hour and minute digitally
• distance - measurement of space between two objects or locations
• extrapolation - the process of estimating an unknown value that exists outside a sequence of data points
• height - vertical measurement between the base of an object and its top
• length - measurement of a figure or object from end to end
• line plot - number line graph that shows frequency of data
• measurable attribute - characteristic that allows a shape or object to be measured (height, width, depth)
• money math - math equations that use units of money
• perimeter - total distance around a shape
• picture graph - graph that uses images or symbols to represent data points
• time interval - amount of time between two set points, indicated in units of time (seconds, minutes, hours)
• unit conversion - converting a unit of measurement into another unit with multiplication or division
• unit square - square unit; unit for measuring area of a two-dimensional shape
• volume - measurement that indicates how much space an object occupies
• width - horizontal measurement that indicates how wide an object or figure is

Sharpen your geometry knowledge by identifying shapes and learning basic terminology:

• 2-D shapes - flat figure with two dimensions (length and width); also known as a figure
• 3-D shapes - solid figure with three dimensions (length, width, and depth)
• angle - two rays that share the same endpoint and are identified by their degrees (e.g. right angles measure exactly 90º, acute angles measure less than 90º)
• axes - the perpendicular lines on a coordinate plane (x-axis and y-axis)
• circumference - total distance around a circle
• coordinate - an ordered pair of numbers that notes a point’s location on a coordinate plane (e.g. -4, 6; 3, -7)
• coordinate plane - plane created by two perpendicular lines (axes) that meet at the origin; area where students can graph coordinate pairs
• defining attributes - characteristics that define a specific shape (e.g. number of sides or angles)
• degree - unit of an angle’s measure noted with the º sign (0 - 360º)
• fourth - one piece of four (the whole); half of a half; a quarter
• geometry - study of shapes and sizes of figures, as well as their lines, angles, and properties
• half - one equal part of a shape or number divided into two parts
• line - straight path that extends in two directions, joining various points along the path
• line segment - straight path with two endpoints
• non-defining attributes - characteristics that don’t define a specific shape (e.g. color, size)
• orientation - position of a shape or figure
• parallel lines - two lines that are always the same distance apart and never intersect
• parallelogram - four-sided figure with opposite parallel sides
• perpendicular line - two lines that intersect at a 90º (right) angle
• plane - flat surface joined by a set of points
• point - a position on a plane, joined by a line
• polygon - shape created by connected line segments
• quadrant - a quarter of a plane that’s divided into four sections
• quadrilateral - four-sided figure
• radius - length of a line segment between the center of a circle and its perimeter
• ray - straight line with one endpoint
• side - line segment between two vertices of a two-dimensional shape, or a face of a three-dimensional shape
• vertices - angular points of a shape

Ratio and proportional relationship terms apply to statistics and probability later on. Some math words relating to ratios and proportional relationships include:

• event - an outcome of probability
• frequency - number of times an event can occur in a period of time
• linear association - proportional relationships between two variables in which one change affects each variable equally; when graphed, these variables form a straight line
• negative association - proportional relationships in which one variable changes in the opposite direction as another variable
• nonlinear association - proportional relationship in which a change in one variable does not equally affect another variable
• odds - likelihood of an event happening, measured in a ratio (the likelihood:total possibilities); also known as probability
• outliers - data point that differs from the behavior of the rest of a data set
• percent - parts of 100 (the whole); fraction with 100 as the denominator
• probability - likelihood of an event happening; also known as odds
• proportional relationship - connection between two variables with equivalent ratios
• positive association - proportional relationship in which a change in one variable causes its value and the value of another variable to increase
• rate - occurrence of an event over a specified period of time
• ratio - comparison of values between two amounts
• relative frequency - number of times an event can occur divided by all possible outcomes
• scatter plot (scatter chart, scatter graph) - graph that uses dots to represent numeric variables between vertical and horizontal axes